受験数学SetUpでは、赤本や各種サイトのわかりにくい解説を直し、どこよりもためになる解説をしています。
今回のポイントはこちら
- 複素数(平面)の扱いに慣れる
- 等式を読み取る力と不等式を使った条件決定力を養う
問題
\(a, b\)を実数とし、\(f (z) = z^2 + az + b \)とする。\(a, b\)が\( |a| \leqq 1, |b| \leqq 1\)を満たしながら動くとき、\(f (z) = 0\)を満たす複素数zが取りうる値の範囲を複素数平面上に図示せよ
条件の整理とゴールの設定
数学の問題はまず条件を整理とゴールの設定します。
条件の整理はなるべく日本語を使わず、数式だけで表し、複雑なものはわかりやすく書き換えます。
\(z^2 + az + b = 0 … ①, zは複素数\)
\(|a| \leqq 1\)
\(|b| \leqq 1 \)
そしてゴールは複素数平面を書くところですね。複素数平面に図示するということは円や直線といった式をzを使って表すということになります。これを条件式から導いていきましょう。
ポイント1:複素数zについて条件分岐
まず重要ポイントが最初にあります。今回はzは「複素数」と言われています。複素数は必ずしも虚数とは限らず、実数の場合も含まれます。これによって条件式の扱い方が変わってくるのでここに注意しましょう。
(i) zが実数の時
まずzが実数の時、①は2次方程式なので解の公式からzはこうなります。
\(z = \dfrac{-a \pm \sqrt{a^2 – 4b}}{2} \)
a,bの条件からこのzの最小と最大の値を考えれば実数の取りうる値の範囲が定まります。
見るべき部分は
\(-a \pm \sqrt{a^2 – 4b}\)
ですね。2変数の最大・最小はまず片方を考えることが大事です。ここではまずaだけに着目しましょう。
最小は
\(-a – \sqrt{a^2 – 4b}\)
でとにかくマイナスが大きくなればいいですね。
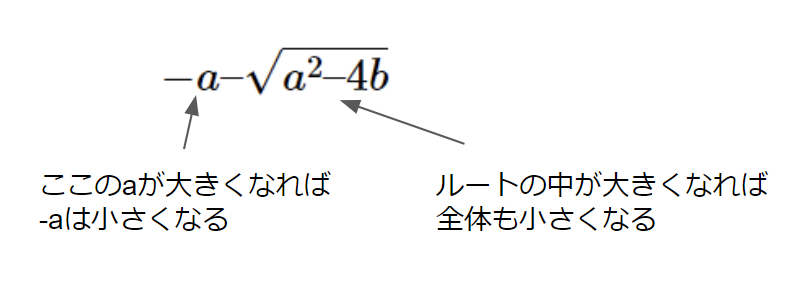
つまり、\(a = 1\)であれば、最初の-(a\)は小さく、またルートの中身も最大になる(つまり全体が最小になる)最低条件が整います。
\(-1 – \sqrt{1}{-4b}\)
次にbを考えると、同じようにルートの中身を最大にすればいいので、\(b = -1\)のときに最大、つまり全体は最小になります。
なのでまず\(z\)の最小は\( – \dfrac{1 + \sqrt{5}}{2}\)となりました。
次は最大です。これはもう一方の
\(-a + \sqrt{a^2 – 4b}\)
を考えば良いですね。
やり方は同じです。\(-a\)が大きくなるように、そしてルートの中身も大きくなるように考えれば良いです。これは\(a = -1, b = -1 \)のときに最大値\(\dfrac{1 + \sqrt{5}}{2}\)なりますね。
なのでzが実数の時取りうる値は
\( – \dfrac{1 + \sqrt{5}}{2} \leqq z \leqq \dfrac{1 + \sqrt{5}}{2} \)
(ii) zが虚数の時
①の式の共役を取ると
\(\bar{z} ^2 + a\bar{x} + b = 0\)
これと①を引いて
\(z^2 – \bar{z}^2 + a(z – \bar{z}) = 0\)
\(\therefore ( z – \bar{z} )a = – ( z + \bar{z} )(z – \bar{z})\)
ここで\(z – \bar{z}\ \neq 0\)です。理由はzが今は実数ではない場合を考えているからです。ここについては重要な部分でもあるんで最後に解説をします。
両辺を\(\(z – \bar{z} \)で割ると
\( a = – (z + \bar{z}) \)。
これと①の式から
\(b = z \bar{z} = |z|^2 \)
となります。
この\( z \bar{z} = |z|^2 \)も重要な式なので覚えておきましょう。これについても最後に解説をします。
さて、\( a = – (z + \bar{z}) \)についてですが、\( (z + \bar{z})\)はzの実数部分\(Re(z)\)をもいいて、\(2Re(z)\)と表せます。これも重要です。最後に解説しますね。
なのでa,bの条件式も踏まえると
\( |-2Re(z)| \leqq 1 \)
\( |z|^2 <\leqq 1\)
つまり
\( \dfrac{1}{2} \leqq Re(z) \leqq \drac{1}{2} \)
\( |z| < \leqq 1\)
下の式は複素平面上で原点が中心の半径1の円です。ここに上の式、つまり実部が-1/2から1/2までの範囲という条件が付きます。
ということで、ここまでの条件をまとめて、zの範囲は以下のようになり、これが答えです。
ただし境界線を含む。
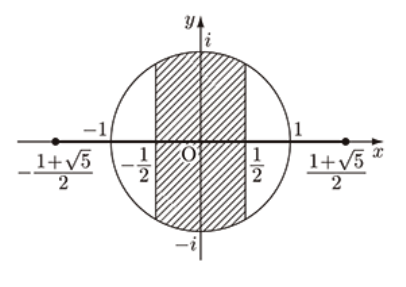
今回は複素数の扱いと範囲の評価が重要でしたね。
複素数における重要ポイント
では今回出てきた重要ポイントの解説をします。
複素数の実数条件と純虚数条件
先ほど\(z – \bar{z}\ \neq 0\)がありましたね。これは以下が成り立つからです。
複素数の実数条件・純虚数条件
\(複素数zが実数 \Leftrightarrow z = \bar{z} \)
\(複素数zが純虚数 \Leftrightarrow z = – \bar{z} \)
これは複素数が実数かどうかをわざわざ\(z = a + bi\)のように置かずとも判別できるので便利
\(z = a + bi\)とおくと、
zが実数なら\(b = 0\)です。なので\(z = \bar{z}\)は明らかですね。
逆に\(z = \bar{z}\)のとき、
\(a + bi = a – bi\)
\(2bi = 0\)
これを満たすには\(b = 0\)となり、zは実数になり証明できました。
純虚数のほうも同じようにできるのでぜひやってみてください。
これを覚えておくとわざわざ\(z = a + bi\)とおいて考える必要がなく、シンプルに複素数\(z\)だけで考えることができるので便利です。
虚数の実部と虚部について
\( z + \bar{z} = 2Re(z) \)というのがありました。これも重要なので押さえておきましょう。
虚数の実部と虚部
複素数zの実部を\( Re(z) \), 虚部を\(Im(z)\)とすると
\( z + \bar{z} = 2Re(z) \)
\( z – \bar{z} = 2Im(z) \)
これは複素数が実数かどうかをわざわざ\(z = a + bi\)のように置かずとも判別できるので便利
\(z = a + bi\)とおくと
\( z + \bar{z} = a + bi + a – bi = 2a \)。
aが実部ですから\(Re(z)\)に置き換えて
\( z + \bar{z} = 2Re(z) \)。
虚部の方も同じですね。
これも先ほどと同様、わざわざ\(z = a + bi\)とおいて考える必要がなく、zのみで評価できるので便利です。
複素数zの大きさ(距離)と図形について
\( z\bar{z} = |z|^2\)が今回出てきました。これも重要ですので抑えましょう。
複素数の大きさと円
複素数\(z = a + bi\)について、\(|z|\)は大きさ、複素数平面で原点からの距離を表す。
\(|z|^2 = z\bar{z} = a^2 + b^2
\(|z| = r\)と表されるとき、これは複素数平面上で原点が中心に半径rの円を表す。
\(z \bar{z} = (a + bi)(a – bi) = (a^2 + b^2) = |z|^2\)となります。
この式は頻出なので絶対に覚えましょう。
この|z|が複素数平面上で原点からの距離を表します。
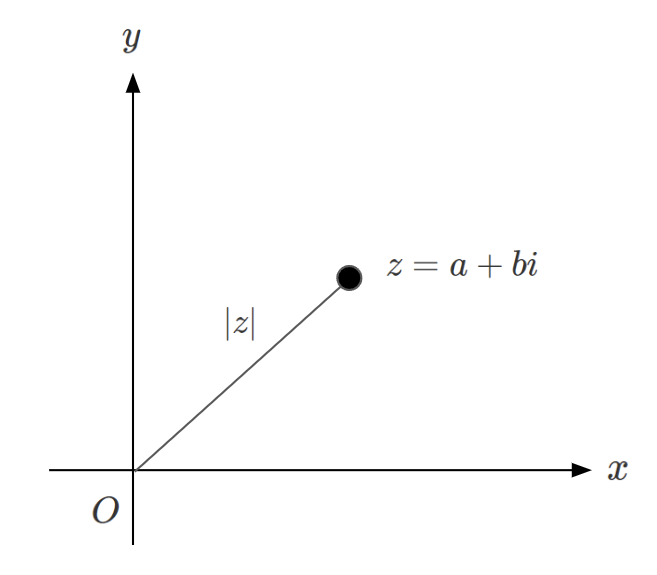
さて、原点からの距離の話になったら何を思い浮かべますか?
そうです、円です。
原点からの距離が一定、つまり\(|z| = r\)と表せるとき、zは円を表します。
xy平面でも\(x^2 + y^2 = r\)が円の式でしたね。これと全く同じです。
先ほど\(|z| \leqq 1\)と出てきましたね。これはまさに円を表し、不等式なのでその内部の領域を表していますね。
複素数の式からグラフや図形につなげられるような訓練は必ずつけましょう
この問題の評価
今回は基礎がわかっていれば、問題なく解ける内容だと思います。
問題を紐解いていくと、複素数の計算と領域の評価だけですからね。
しかし、複素数平面は苦手にする学生も多いですし、上記の場合分けなどでつまづく人は多いのではないかと思います。
5,6年前は複素数平面はそこまで主流ではないですが、ここ数年で頻出レベルまで見るようになったので複素数平面も必ず押さえておきましょう。
コメント