数学では「0で割ってはいけない」は共通認識になっています。
しかし、これをなぜ?と深く考えたことはありますか?
「お菓子を0人で分けるって意味わからないじゃん。だから0で割れない」
これは解答としては不正解です。
なぜ1,2では割れて、0では割れないのか。
ここでは0で割れない理由を深く考え、それにより高校数学でも重要な考え方につながっていきますのでぜひ最後まで読んでください。
その1:演算が定義されない
計算ができる(演算ができる)の定義は「2つの数からただ一つの値が求まる操作」とされています。直感的にもわかることですね。
\(1+1 = 2\)
\(2^3 = 8\)
\(24 / 4 = 6\)
\(\sum ^{10}_{k=1}k = 55 \)
上記はすべて演算ができています。1と1を足すという操作(左辺)により2(右辺)という唯一の値に求まりました。他も同じですね。
では0で割る場合も考えてみます。
演算ができると仮定してみると、定義の通り何らかの値が求まるので、その値をxとして
\(a / 0 = x \)
とおけます。
ここでaについて場合分けして考えてみます。
\(a \neq 0\)のとき
両辺に0をかけてあげると、
\(a = x \cdot 0\)
さて、いま\(a \neq 0\)としているのでこれを満たすxは何でしょう?
・・・
ありませんね。
どんなxを入れても0をかけているので0になってしまいます。
最初の過程でxは存在すると決めていたことに反していますね。
\(a = 0\)のとき
\(0 = x \cdot 0\)
このようになりますね。これを満たすxは何でしょう?
先ほどとは逆に、どんなxでも式が成り立ちます。
これもxはただ一つに決まるということに反していますね。
ゼロで割ることは答えがただ一つに定まらない、つまり演算ができいので、「0で割ってはいけない」のです。
その2 : グラフを考えてみる
今は定義から考えてみました。
今度は直感的に、視覚的にわかるように考えてみます。
\(y = a / x\)を考えてみます。これは反比例のグラフですね。中学の時に習ったかと思います。
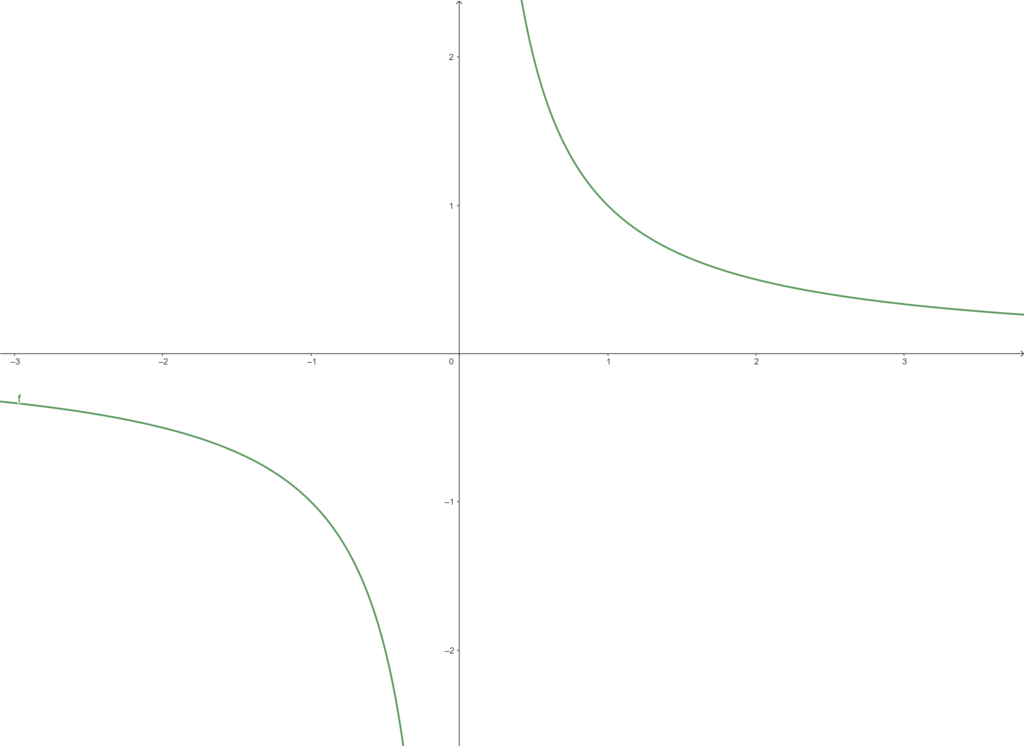
0で割る、つまり\(x=0\)となる部分を見てみましょう。
正の方向を見ると、y軸に徐々に近づきますが、交わることはありません。
負の方向を見ても同様ですね。
交わることがないということは、極限まで値が大きくなる。つまり無限大ということになります。
なので0で割るということはできないのです。
「0で割ることができない」は常に意識しておくこと
0で割れないということはずっと言われてきたことですから知っているかと思います。
しかし、高校数学になるとこのことが非常に重要です。
その理由を教えます。
文字式を使った計算が多くなるため
高校生になると中学よりも文字を使った計算が多くなってきます。
そして分母に文字がある場合、0ではないと意識しなくても理解できます。
そこでこんな問題を見てください。
「方程式 \(ax^2 + bx + c = 0\) (\(b \neq 0\))を解け」
見ての通り2次方程式の形をしているので、解の公式をそのまま答えればOKです。
\(x = \dfrac{-b\pm \sqrt{b^2-4ac}}{2a}\)
とやってしまうと0点です。
ここまでやってきていればわかりますね。
aが0である場合もあるからです。上記式は「方程式」としか書かれていません。2次方程式と書かれていない以上、aは0である可能性もあります。
なのでこれはaが0かそうでないかで場合分けが必要なのです。
\(a = 0\)のとき、\(x = c / b\)
\(a \neq = 0\)のとき、\(x = \dfrac{-b\pm \sqrt{b^2-4ac}}{2a}\)
このように、先入観により文字が0である可能性を忘れて割ってしまう間違いが非常に多いので注意しましょう。
0で割ることは極限値に関係する
0で割ることはできませんが、「0に限りなく近づける」という操作はできます。これがまさに数Ⅲで学ぶ「極限」です。
先ほどの\(y = a / x\)でxを0に限りなくyは正にあるいは負に限りなく大きくなっていきます。
この感覚で極限値は求めていきます。この場合(\(a \neq 0\))極限値は
\(\lim _{x\rightarrow \pm 0}\dfrac{a}{x}=\pm \infty\)
となります。
(\(a = 0\)\)の場合、先ほど見たようにどんな値でも取り得ます。
このいわゆる\(0 / 0\)の形を不定形と言い、式の形によって極限値が求まったり求まらなかったりします。うまく式変形して\(0 / 0\)の形から抜け出すようにします。
この0で割ったら無限大、\(0/0\)は不定形というのも、もともとはこの「0で割ってはいけない理由」からきているんですね。
そういえばなぜ?を大切に
いかがでしたか?
0で割れないというのが当たり前になっているので、いざ理由を考えると面白いですよね。
「お菓子を0人で分けるって意味わからないじゃん。だから0で割れない」なんて説明では、不十分で、極限値まで話が進まずに終わって今います。
このように数学で当たり前のようにやってきたことを一度振り返ってみると意外な結びつきが見えてきたりします。
受験数学SetUpでは受験のノウハウを教えていきますが、このような理解を深めるためのコラムも紹介していきますので、ぜひ定期的に読んでみてください!
コメント